대응비교 t 검정
- 귀무가설 : 운동 전후 집중력 평균의 차이가 없을 것이다. (전=후)(귀무가설은 무조건 차이가 없다)
- 대립가설 : 운동 전후 집중력 평균의 차이가 있을 것이이다. (전!=후)
<1sample t test 방식>
** 1sample t test : 한 집단의 평균이 기대값과 같은지를 검정
1. 데이터 불러오기
우선 데이터를 불러오고 전후 차 값을 나타내는 열을 추가함
import pandas as pd
training_rel = pd.read_csv('data/ch11_training_rel.csv')
training_rel['차'] = training_rel['후'] - training_rel['전']
training_rel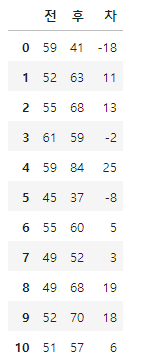
2. scipy의 ttest_1sample 함수로 t 검정 통계량과 p 값을 구함
t_statistic, p_value = stats.ttest_1samp(sample_data, popmean=expected_mean)
"운동 전후 집중력 평균의 차이가 없을 것이다"라는 귀무가설을 검정하고자 하는 것이므로
popmean=0은 귀무가설에서 주장하는 운동 전후 평균의 차이가 0이라는 가정을 표현
from scipy import stats
t, p = stats.ttest_1samp(training_rel['차'],0)
t, p
=> 결론 : p 값이 0.04로 유의수준(0.05)보다 작기 때문에 귀무가설 기각!
<대응표본 방식>
** 두 개의 표본에서 나온 데이터를 기반으로, 두 표본 간의 평균 차이가 통계적으로 유의미한지를 평가
이 함수를 쓰면 굳이 차이 값을 구하지 않아도 됨
t_statistic, p_value = stats.ttest_rel(sample1, sample2)
t, p = stats.ttest_rel(training_rel['후'], training_rel['전'])
t, p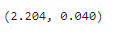
=> 결론 : p 값이 0.04로 유의수준(0.05)보다 작기 때문에 귀무가설 기각!
독립비교 t 검정
- 귀무가설 : A 그룹과 B 그룹 간의 집중력 평균의 차이가 없을 것이다.
- 대립가설 : A 그룹과 B 그룹 간의 집중력 평균의 차이가 있을 것이다.
t_statistic, p_value = stats.ttest_ind(sample1, sample2, equal_var=True)
stats.ttest_ind() 함수는 두 독립적인 그룹 간의 평균 차이를 비교하는 데 사용되며, 이는 두 그룹이 서로 독립적이고, 짝을 이루지 않는 경우에 적용됩니다. 만약 짝을 이룬 데이터가 있다면, stats.ttest_rel() 함수를 사용하는 것이 더 적절!
equal_var= True는 두 그룹의 분산이 동일하다고 가정 (등분산성을 가정)하는 옵션 /False로 설정하면 등분산성을 가정하지 않는 옵션
1. 우선 데이터 불러옴
training_ind = pd.read_csv('data/ch11_training_ind.csv')
training_ind.head()
2. t와 p 값 구하기
- 등분산성이 같을 경우
t, p = stats.ttest_ind(training_ind['A'], training_ind['B'], equal_var = True)
t, p
=> 결론 : p 값이 0.086으로 유의수준(0.05)보다 크기 때문에 귀무가설 채택!
- 등분산성이 다를 경우 ( 등분산성은 levene 검정으로 확인)
t, p = stats.ttest_ind(training_ind['A'], training_ind['B'], equal_var = False)
t, p
=> 결론 : p 값이 0.086으로 유의수준(0.05)보다 크기 때문에 귀무가설 채택!
'Python > 통계' 카테고리의 다른 글
| 카이제곱 독립성검정 예시 (0) | 2024.01.14 |
|---|---|
| 단순회귀분석 예시 (0) | 2024.01.14 |
| 비모수검정 - 윌콕슨의 부호순위검정 (0) | 2024.01.13 |
| t-test, One Sample T-test 양측검정과 단측검정 (1) | 2024.01.11 |
| 통계 개념 정리 (1) | 2024.01.10 |