[분류] 신용카드 사기 검출

분류 실습 - 신용카드 사기 검출

1. 데이터 1차 가공 및 모델 학습/예측/평가 - 로지스틱회귀분석

1. 데이터 불러오기

import pandas as pd
import numpy as np 
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")
%matplotlib inline

card_df = pd.read_csv('./creditcard.csv')
card_df.head(3)

 

card_df.shape

 

2. 데이터 복사 후, 불필요한 데이터 삭제 및 학습과 테스트 데이터로 분할

from sklearn.model_selection import train_test_split

# 인자로 입력받은 DataFrame을 복사 한 뒤 Time 컬럼만 삭제하고 복사된 DataFrame 반환
def get_preprocessed_df(df=None):
    df_copy = df.copy()
    df_copy.drop('Time', axis=1, inplace=True)
    return df_copy
    
# 사전 데이터 가공 후 학습과 테스트 데이터 세트를 반환하는 함수.
def get_train_test_dataset(df=None):
    # 인자로 입력된 DataFrame의 사전 데이터 가공이 완료된 복사 DataFrame 반환
    df_copy = get_preprocessed_df(df)
    
    # DataFrame의 맨 마지막 컬럼이 레이블, 나머지는 피처들
    X_features = df_copy.iloc[:, :-1]
    y_target = df_copy.iloc[:, -1]
    
    # train_test_split( )으로 학습과 테스트 데이터 분할. stratify=y_target으로 Stratified 기반 분할
    X_train, X_test, y_train, y_test = \
    train_test_split(X_features, y_target, test_size=0.3, random_state=0, stratify=y_target)
    
    # 학습과 테스트 데이터 세트 반환
    return X_train, X_test, y_train, y_test

X_train, X_test, y_train, y_test = get_train_test_dataset(card_df)

 

stratified 기반으로 분할하였으며, 학습 데이터와 테스트 데이터의 레이블 값 비율을 확인해보면 동일한 것을 확인할 수 있음

print('학습 데이터 레이블 값 비율')
print(y_train.value_counts()/y_train.shape[0] * 100)
print('테스트 데이터 레이블 값 비율')
print(y_test.value_counts()/y_test.shape[0] * 100)

 

3. 로지스틱회귀분석 후 평가 수행

from sklearn.metrics import confusion_matrix, accuracy_score, precision_score, recall_score, f1_score
from sklearn.metrics import roc_auc_score

# 평가를 위한 함수 생성
def get_clf_eval(y_test, pred=None, pred_proba=None):
    confusion = confusion_matrix( y_test, pred)
    accuracy = accuracy_score(y_test , pred)
    precision = precision_score(y_test , pred)
    recall = recall_score(y_test , pred)
    f1 = f1_score(y_test,pred)
    # ROC-AUC 추가 
    roc_auc = roc_auc_score(y_test, pred_proba)
    print('오차 행렬')
    print(confusion)
    # ROC-AUC print 추가
    print('정확도: {0:.4f}, 정밀도: {1:.4f}, 재현율: {2:.4f},\
    F1: {3:.4f}, AUC:{4:.4f}'.format(accuracy, precision, recall, f1, roc_auc))


# 로지스틱회귀분석으로 학습 및 예측하고 평가 수행
from sklearn.linear_model import LogisticRegression

lr_clf = LogisticRegression(max_iter=1000)
lr_clf.fit(X_train, y_train)
lr_pred = lr_clf.predict(X_test)
lr_pred_proba = lr_clf.predict_proba(X_test)[:, 1]

# 3장에서 사용한 get_clf_eval() 함수를 이용하여 평가 수행. 
get_clf_eval(y_test, lr_pred, lr_pred_proba)

 

☢️정확도: 0.9992, 정밀도: 0.8654, 재현율: 0.6081,    F1: 0.7143, AUC:0.9704

 

2. LightGBM 학습/예측/평가

1. 피처 엔지니어링 수행할 때마다 모델을 학습/예측/평가하므로 이를 위한 함수 생성

# 인자로 사이킷런의 Estimator객체와, 학습/테스트 데이터 세트를 입력 받아서 학습/예측/평가 수행.
def get_model_train_eval(model, ftr_train=None, ftr_test=None, tgt_train=None, tgt_test=None):
    model.fit(ftr_train, tgt_train)
    pred = model.predict(ftr_test)
    pred_proba = model.predict_proba(ftr_test)[:, 1]
    get_clf_eval(tgt_test, pred, pred_proba)

 

2. LightGBM 학습/예측/평가

• LightGBM 2.1.0 이상 버전에서 boost_from_average가 True가 Default가 됨.
• boost_from_average가 True일 때, 레이블 값이 극도로 불균형 분포를 이루는 경우 재현률 및 ROC-AUC 성능이 매우 저하됨. 레이블 값이 극도로 불균형할 경우 boost_from_average를 False로 설정하는 것이 유리
• 레이블 데이터가 불균형하므로 boost_from_average를 False로 설정하여 진행

from lightgbm import LGBMClassifier

lgbm_clf = LGBMClassifier(n_estimators=1000, num_leaves=64, n_jobs=-1, boost_from_average=False)
get_model_train_eval(lgbm_clf, ftr_train=X_train, ftr_test=X_test, tgt_train=y_train, tgt_test=y_test)

 

☢️정확도: 0.9995, 정밀도: 0.9573, 재현율: 0.7568, F1: 0.8453,  AUC:0.9790

📌 LGBM으로 모델 변경 후 평가 지표 상승함

3. 데이터 분포도 변환 후 모델 학습/예측/평가

feature들 중 나머지는 PCA가 되어있지만 Amount 피처의 경우 가공되지 않음

feature의 분포도 확인 후 정규 분포로 변환하여 모델 학습/예측/평가 진행

 

1. 피처 분포도 확인

import seaborn as sns

plt.figure(figsize=(8, 4))
plt.xticks(range(0, 30000, 1000), rotation=60)
sns.histplot(card_df['Amount'], bins=100, kde=True)
plt.show()

📌 왼쪽으로 skrew되어있음

 

2. StandardScaler를 이용하여 Amount 피처 변환

피처 변환 → 데이터 분리 → 학습/예측/평가

# 데이터 사전 가공을 위한 별도의 함수에 StandardScaler를 이용하여 Amount 피처 변환

from sklearn.preprocessing import StandardScaler
# 사이킷런의 StandardScaler를 이용하여 정규분포 형태로 Amount 피처값 변환하는 로직으로 수정. 
def get_preprocessed_df(df=None):
    df_copy = df.copy()
    scaler = StandardScaler()
    amount_n = scaler.fit_transform(df_copy['Amount'].values.reshape(-1, 1))
    # 변환된 Amount를 Amount_Scaled로 피처명 변경후 DataFrame맨 앞 컬럼으로 입력
    df_copy.insert(0, 'Amount_Scaled', amount_n)
    # 기존 Time, Amount 피처 삭제
    df_copy.drop(['Time','Amount'], axis=1, inplace=True)
    return df_copy
    
StandardScaler 변환 후 로지스틱 회귀 및 LightGBM 학습/예측/평가
# Amount를 정규분포 형태로 변환 후 로지스틱 회귀 및 LightGBM 수행. 
X_train, X_test, y_train, y_test = get_train_test_dataset(card_df)

print('### 로지스틱 회귀 예측 성능 ###')
lr_clf = LogisticRegression(max_iter=1000)
get_model_train_eval(lr_clf, ftr_train=X_train, ftr_test=X_test, tgt_train=y_train, tgt_test=y_test)

print('### LightGBM 예측 성능 ###')
lgbm_clf = LGBMClassifier(n_estimators=1000, num_leaves=64, n_jobs=-1, boost_from_average=False)
get_model_train_eval(lgbm_clf, ftr_train=X_train, ftr_test=X_test, tgt_train=y_train, tgt_test=y_test)

 

☢️로지스틱 회귀 - 정확도: 0.9992, 정밀도: 0.8654, 재현율: 0.6081, F1: 0.7143,  AUC:0.9702

☢️LGBM - 정확도: 0.9995, 정밀도: 0.9569, 재현율: 0.7500, F1: 0.8409,  AUC: 0.9779

📌standardscaler 사용했을 때 전보다 나아진 것이 없음

 

3. Log변환하여 Amount 피처 변환

def get_preprocessed_df(df=None):
    df_copy = df.copy()
    # 넘파이의 log1p( )를 이용하여 Amount를 로그 변환 
    amount_n = np.log1p(df_copy['Amount'])
    df_copy.insert(0, 'Amount_Scaled', amount_n)
    df_copy.drop(['Time','Amount'], axis=1, inplace=True)
    return df_copy

X_train, X_test, y_train, y_test = get_train_test_dataset(card_df)

print('### 로지스틱 회귀 예측 성능 ###')
get_model_train_eval(lr_clf, ftr_train=X_train, ftr_test=X_test, tgt_train=y_train, tgt_test=y_test)

print('### LightGBM 예측 성능 ###')
get_model_train_eval(lgbm_clf, ftr_train=X_train, ftr_test=X_test, tgt_train=y_train, tgt_test=y_test)

 

로그변환 후 완벽한 정규분포는 아니지만 skrew되어있던게 개선됨

import seaborn as sns

plt.figure(figsize=(8, 4))
sns.histplot(X_train['Amount_Scaled'], bins=50, kde=True)
plt.show()

 

☢️로지스틱 회귀 - 정확도: 0.9992, 정밀도: 0.8812, 재현율: 0.6014, F1: 0.7149, AUC:0.9727

☢️LGBM - 정확도: 0.9995, 정밀도: 0.9576, 재현율: 0.7635, F1: 0.8496, AUC:0.9796

📌log 변환도 크게 나아진 것이 없음

4. 이상치 데이터 제거 후, 로그변환하여 모델 학습/예측/평가

상관분석하여 레이블값인 Class와 높은 상관관계를 보이는 값의 이상치 데이터를 제거 후 모델 학습

1. 상관분석하여 상관관계 높은 데이터 확인

import seaborn as sns

plt.figure(figsize=(12, 12))
corr = card_df.corr()
sns.heatmap(corr, annot=True, fmt='.1f',  cmap='RdBu')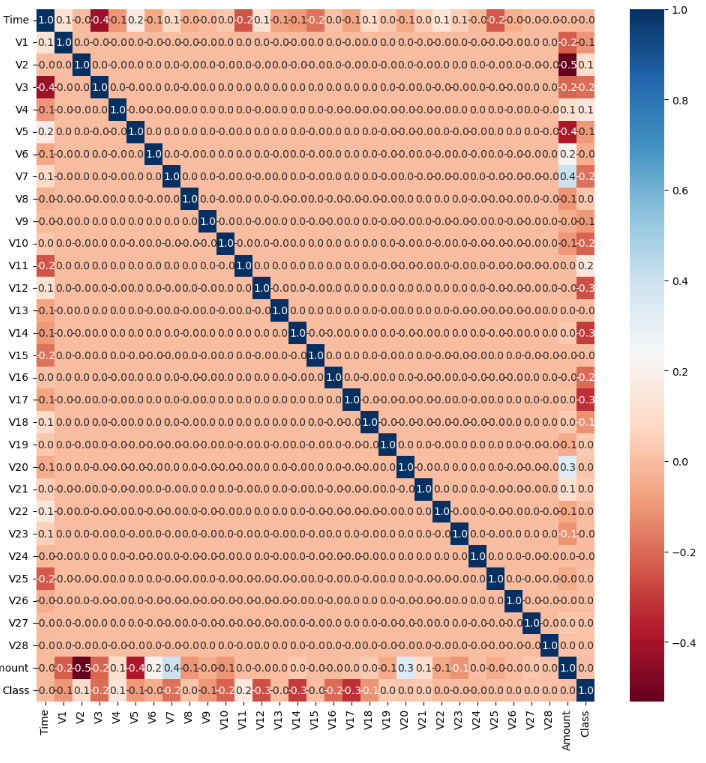

class와 v14, v17, v12의 상관관계가 가장 높음

이 중에서 v14만 outlier 제거

 

2. v14 컬럼의 outlier 인덱스 추출

Dataframe에서 outlier에 해당하는 데이터를 필터링하기 위한 함수 생성. outlier 레코드의 index를 반환함

프로드는 프로드에 해당하는 것만 찾을것이기 때문에, 사기거래가 1일때의 이상치만 제거

import numpy as np

def get_outlier(df=None, column=None, weight=1.5):
    # fraud에 해당하는 column 데이터만 추출, 1/4 분위와 3/4 분위 지점을 np.percentile로 구함. 
    fraud = df[df['Class']==1][column]
    quantile_25 = np.percentile(fraud.values, 25)
    quantile_75 = np.percentile(fraud.values, 75)
    # IQR을 구하고, IQR에 1.5를 곱하여 최대값과 최소값 지점 구함. 
    iqr = quantile_75 - quantile_25
    iqr_weight = iqr * weight
    lowest_val = quantile_25 - iqr_weight
    highest_val = quantile_75 + iqr_weight
    # 최대값 보다 크거나, 최소값 보다 작은 값을 아웃라이어로 설정하고 DataFrame index 반환. 
    outlier_index = fraud[(fraud < lowest_val) | (fraud > highest_val)].index
    return outlier_index

outlier_index = get_outlier(df=card_df, column='V14', weight=1.5)
print('이상치 데이터 인덱스:', outlier_index)

3. 로그 변환 후 v14 피처의 outlier 데이터 삭제한 뒤 모델들을 재 학습/예측/평가

# get_processed_df( )를 로그 변환 후 V14 피처의 이상치 데이터를 삭제하는 로직으로 변경. 
def get_preprocessed_df(df=None):
    df_copy = df.copy()
    amount_n = np.log1p(df_copy['Amount'])
    df_copy.insert(0, 'Amount_Scaled', amount_n)
    df_copy.drop(['Time','Amount'], axis=1, inplace=True)
    # 이상치 데이터 삭제하는 로직 추가
    outlier_index = get_outlier(df=df_copy, column='V14', weight=1.5)
    df_copy.drop(outlier_index, axis=0, inplace=True)
    return df_copy

X_train, X_test, y_train, y_test = get_train_test_dataset(card_df)
print('### 로지스틱 회귀 예측 성능 ###')
get_model_train_eval(lr_clf, ftr_train=X_train, ftr_test=X_test, tgt_train=y_train, tgt_test=y_test)
print('### LightGBM 예측 성능 ###')
get_model_train_eval(lgbm_clf, ftr_train=X_train, ftr_test=X_test, tgt_train=y_train, tgt_test=y_test)

☢️로지스틱 회귀 - 정확도: 0.9993, 정밀도: 0.8750, 재현율: 0.6712, F1: 0.7597, AUC:0.9743

☢️LGBM - 정확도: 0.9996, 정밀도: 0.9603, 재현율: 0.8288, F1: 0.8897, AUC:0.9780

 

📌이상치 제거 후 성능 좋아짐 

이상치 제거는 최대한 덜 지우고, 정말 어떤 기준상에서 좀 많이 벗어난다 싶은 정도만 적게 지워야 함

모델 성능은 좋아지겠지만 어떤 테스트 데이터가 그런 유형에 들어올 수 있기 때문! 

5. SMOTE 오버 샘플링 적용 후 모델 학습/예측/평가

y_train.value_counts()

레이블 값의 분포 차이가 큼

 

1. SMOTE 오버 샘플링

import imblearn
from imblearn.over_sampling import SMOTE

smote = SMOTE(random_state=0)
X_train_over, y_train_over = smote.fit_resample(X_train, y_train)
print('SMOTE 적용 전 학습용 피처/레이블 데이터 세트: ', X_train.shape, y_train.shape)
print('SMOTE 적용 후 학습용 피처/레이블 데이터 세트: ', X_train_over.shape, y_train_over.shape)
print('SMOTE 적용 후 레이블 값 분포: \n', pd.Series(y_train_over).value_counts())

 

2. 로지스틱 회귀분석으로 데이터 학습/예측/평가

✍️학습만 오버샘플링한 데이터로 학습, 테스트는 원본데이터로!! 

lr_clf = LogisticRegression(max_iter=1000)
# ftr_train과 tgt_train 인자값이 SMOTE 증식된 X_train_over와 y_train_over로 변경됨에 유의
get_model_train_eval(lr_clf, ftr_train=X_train_over, ftr_test=X_test, tgt_train=y_train_over, tgt_test=y_test)

📌재현율은 좋아졌지만 정밀도 크게 낮아짐

 

precision, recall 그래프 그려보면 recall은 좋지만, precision은 안올라오는 모습을 보임

import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
from sklearn.metrics import precision_recall_curve
%matplotlib inline

def precision_recall_curve_plot(y_test , pred_proba_c1):
    # threshold ndarray와 이 threshold에 따른 정밀도, 재현율 ndarray 추출. 
    precisions, recalls, thresholds = precision_recall_curve( y_test, pred_proba_c1)
    
    # X축을 threshold값으로, Y축은 정밀도, 재현율 값으로 각각 Plot 수행. 정밀도는 점선으로 표시
    plt.figure(figsize=(8,6))
    threshold_boundary = thresholds.shape[0]
    plt.plot(thresholds, precisions[0:threshold_boundary], linestyle='--', label='precision')
    plt.plot(thresholds, recalls[0:threshold_boundary],label='recall')
    
    # threshold 값 X 축의 Scale을 0.1 단위로 변경
    start, end = plt.xlim()
    plt.xticks(np.round(np.arange(start, end, 0.1),2))
    
    # x축, y축 label과 legend, 그리고 grid 설정
    plt.xlabel('Threshold value'); plt.ylabel('Precision and Recall value')
    plt.legend(); plt.grid()
    plt.show()
    
precision_recall_curve_plot( y_test, lr_clf.predict_proba(X_test)[:, 1] )

 

3. LGBM으로 학습/예측/평가

✍️학습만 오버샘플링한 데이터로 학습, 테스트는 원본데이터로!! 

lgbm_clf = LGBMClassifier(n_estimators=1000, num_leaves=64, n_jobs=-1, boost_from_average=False)
get_model_train_eval(lgbm_clf, ftr_train=X_train_over, ftr_test=X_test,
                  tgt_train=y_train_over, tgt_test=y_test)

☢️로지스틱 회귀 - 정확도: 0.9723, 정밀도: 0.0542, 재현율: 0.9247,    F1: 0.1023, AUC:0.9737

☢️LGBM - 정확도: 0.9996, 정밀도: 0.9118, 재현율: 0.8493,    F1: 0.8794, AUC:0.9814

 

📌이상치 제거했을 때보다 LGBM에서 정밀도 좀 낮아졌지만 재현율은 상대적으로 좋아짐

사기검출은 재현율 지표가 조금 더 중요한 지표이기 때문에 SMOTE오버샘플링 후 더 모델이 좋아졌다고 평가할 수 있음